Pokud hledáme motivační témata, která mohou popularizovat matematiku, neměli bychom zapomenout na fraktály a jejich geometrické modelování.

Fraktální geometrie vychází z pojmu fraktál. Ten můžeme definovat jako nekonečně členitý útvar, který je geometricky nepravidelný a z něhož po rozdělení vznikne několik pseudokopií původního celku. Tyto útvary jsou nezávislé na měřítku, z matematického pohledu mají nekonečně dlouhý obvod a nekonečně malý obsah.

Některé fraktály jsou abstraktní objekty vytvořené fantazií matematiků, jiné mají vzory přímo v přírodě: břehy potoků, řek, pobřeží ostrovů, plocha mozku, větvení stromů, větvení cév a žil v těle, hromadění bakterií v koloniích, hory, mraky, elektrické výboje, špinavé skvrny, apod. Podle toho už vidíme, že se fraktální geometrie zabývá nepravidelností objektů.

Přiblížení fraktálů

Abychom pochopili, o co vlastně jde, je nutné si představit klasickou Euklidovskou geometrii, kterou známe ze školy, a ve které má každý objekt tzv. dimenzi hodnoty 1 (např. přímka), 2 (např. trojúhelník) nebo 3 (např. jehlan). Uvedená hodnota je vlastně počet parametrů, které jsou potřeba k jednoznačnému určení objektu. Tato dimenze se nazývá topologická.

Ve fraktální geometrii je objekt určován podle tzv. dimenze fraktální neboli Hausdorffovy – Besicovitchovy, která určuje míru nepravidelnosti objektu. Z číselného pohledu se jedná o to, že hodnota dané dimenze je vždy o nějaké to desetinné číslo větší než v dimenzi topologické. Čím je tato dimenze větší v intervalu mezi dvěma celočíselnými hodnotami (0–1, 1-2, 2-3), tím je objekt členitější. A právě takový útvar se nazývá fraktál. Říká se také, že fraktální objekty vzniklé vytvořením kopií původního objektu jsou statisticky soběpodobné.

V podstatě můžeme říct, že např. zvětšením či zmenšením objektu se díky teorii chaosu (náhodnému působení vnějších vlivů) nikdy nedosáhne dokonale věrné kopie. Vzhled těchto objektů zaujme především svou harmonií mezi určitou pravidelností a nahodilostí, podobně jako přírodní útvary, které možná působí chaoticky, přesto u nich vnímáme určitý řád.

Teorie chaosu vlastně říká, že cosi jako zcela úspěšná předpověď nemůže ve složitých jevech vůbec existovat. Pokud by tomu tak totiž bylo, dokázali bychom bez problémů říci, že v Česku na úpatí Krušných hor bude větrná smršť, neboť v Brazílii mávnul motýl křídly, čímž dal příčinu vzniku jevu o několik týdnů zpožděnému. Možná si právě nyní uvědomujeme, že příroda se svým systematicko-chaotickým přístupem neustále brání lidské snaze o vytvoření co nejdokonalejší pravidelnosti právě tím, že její objekty jsou pouze „podobné“.

Fraktály ve výuce

A) Výpočet dimenze

Výchozí rovnice pro určení dimenze má tvar N.r^D=1. Pokud chceme vyjádřit dimenzi D, použijeme logaritmus. Vzhledem k tomu, že logaritmické rovnice při výuce působí poměrně samoúčelně, konečně je k dispozici aplikace do konkrétní situace, navíc početně velmi jednoduchá. Krása rovnice je i ve skutečnosti, že je použitelná pro topologickou dimenzi (doporučuji jednoduché cvičení).

• D – označení fraktální dimenze objektu
• N – faktor změny délky (nový počet úseků)
• r – délka jednoho nově vzniklého dílku při rozdělení původního útvaru či jeho části

Představme si, že máme čtverec (resp. jeho obvod), ve třetině každé jeho strany vytvoříme nový čtverec (bez jedné strany – vznikne tak spojitá lomená čára). V podstatě jsme původní délku strany přetransformovali na 1/3 (r=1/3) původní hodnoty, počet podobných úseků bude 5 (N=5).

N . r^D = 1
r^D = 1/N
D . log r = log (1/N)
D = log (1/N) / log (r) – po úpravě
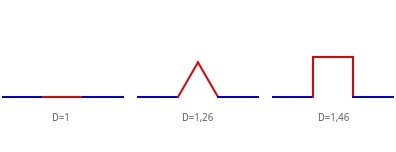
D = log 5 / log 3 = 1,46

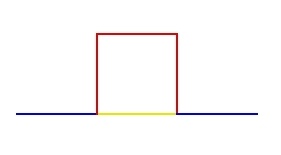
Tato hodnota řadí nově vzniklý útvar někam mezi přímku (D=1) a plochu (D=2). Nově vzniklý útvar bude zřejmě neustálou transformací převeden v objekt, který bude mít ve fraktálovém pojetí nekonečný obvod a jím vymezený obrazec bude mít konečnou plochu. Červená transformace odpovídá prvnímu přiblížení a nahrazuje žlutou část. Místo jedné třetiny původní délky byly přidány tři.

B) Fraktály v informatice

Jednoduché lomené čáry typu „Kochova vločka“ jsou velmi snadno programovatelné v nějakém grafickém prostředí. Nabízí se program KTurtle, neboli želví programování. Tato linuxová platforma je pro algoritmizaci a výuku vhodná již na základní škole a v podobě podobných výstupů opravdu motivující. Z pohledu geometrie jde pouze o systematickou volbu vhodných úhlů a délek, popř. využití cyklů. Vzhledem k jednoduché syntaxi a okamžité zpětné vazbě je možné připravovat snadno programovatelné úlohy.

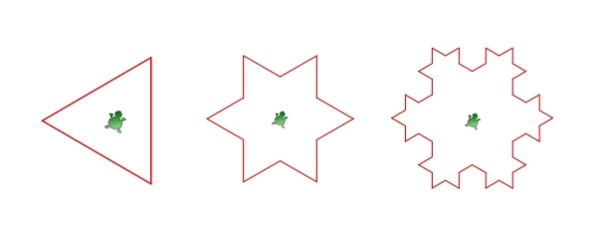
C) Výtvarné nápady

Kromě těchto jednoduchých a snadno matematicky odůvoditelných fraktálů je možné přistoupit k jejich aplikování do výtvarných činností. Počínaje Mandelbrotovou množinou máme k dispozici různé modifikace. I když se jedná o složité struktury vznikající na množině komplexních čísel, mají rovněž své závislosti. Na Internetu existuje řada programů zdarma, které umožňují fraktály tvořit a transformovat.

Několik známých fraktálů

L – systémy

Cantorovo diskontinuum – vznikne postupným dělením úsečky na 3 shodné části. Prostřední vypustíme, a tak postupujeme dál. Délka „nekonečně“ mnoha úseček konvertuje k nule, ale počet bodů jde k nekonečnu. Pomocí výpočtu lze ověřit, že jde o fraktál s dimenzí 0,63 (mezi bodem a lineárním útvarem).

Kochova křivka – na obrázku je vidět, že postupná transformace délku křivky neustále prodlužuje.

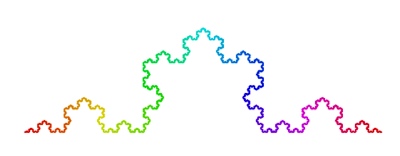
Kochova vločka – k základnímu trojúhelníku přidáme k prostřední třetině každé strany trojúhelník o třetinu menší. Hranicí tohoto vzniklého útvaru je lámaná křivka, která nikdy neprotne sebe sama. Plocha konvertuje ke konkrétní hodnotě, obvod je nekonečně dlouhý. Výpočtem dojdeme k fraktálu s dimenzí 1,26 (mezi lineárním a plošným útvarem). Kochova vločka patří k nejkrásnějším fraktálům, a to především díky jednoduché linii, která se díky podrobnějšímu měřítku mění v zajímavou „ostrovní“ hranici. Ta se s každým zjemněním prodlužuje, i když máme pocit konečnosti.

Sierpinského trojúhelník – z trojúhelníka vyjmeme trojúhelník vytvořený středními příčkami. Toto opakujeme stále u každého nově vzniklého útvaru, až dostaneme nekonečně mnoho trojúhelníků s plochou konvertující k nule.

Mengerova houba – trojrozměrná mřížka, která má nekonečně velký povrch a jejíž objem konvertuje k nule. Představme si krychli, která se skládá z 27 malých krychliček. Vyjmeme 7 z nich tak, aby zmizely prostřední ve stranách a ta uprostřed krychle. V dalším kroku celý postup opakujeme na všech 20 zbylých krychličkách.

Systémy iterovaných funkcí (polynomické fraktály)

Barnsleyho kapradina – nádherný geometrický útvar, kdy se ukazuje, že každý lístek kapradiny je téměř kopií sebe sama. V podstatě vznikl tak, že původní útvar byl postupně doplňován dalšími útvary, které byly zmenšenou kopií původního. Tyto menší útvary byly pokládány tak, že mohly i překrývat původní objekt. Drobné zkreslení je naprosto zanedbatelné, řekl bych, že až žádoucí. Takto vzniklý útvar teprve vedl k pokusu o „zmatematizování“.

Newtonova množina – útvar vznikl grafickým řešením Newtonovy rovnice x³-1=0 v oboru komplexních čísel. Body (modely řešení) vždy v grafickém zobrazení konvertují k určitému kořenu. Při grafickém řešení se na rozhraní ploch určujících řešení objevily další nové obrazce.

Juliova množina – náhodně zvolené komplexní číslo c bude charakterizovat množinu. Každý bod z roviny v komplexním oboru umocníme a přičteme k němu c. V případě, že výsledné číslo konvertuje k nule, patří do Juliovy množiny. Velmi zajímavé je zbarvení množin. Závisí totiž na na počtu iterací potřebných ke zjištění, zda číslo patří do Juliovy množiny.

Mandelbrotova množina – tato množina v komplexní rovině vznikne tak, že v každém svém bodě určuje vzhled Juliovy množiny. K určitému komplexnímu číslu přičteme jeho druhou mocninu. Tento výsledek umocníme a přičteme k němu původní číslo. Pokud výsledek nepřesáhne hodnotu 2, patří bod do množiny. Mohou zde být různé typy množin závislé na zvoleném exponentu, což vede až k neuvěřitelně krásným útvarům. Jinými slovy, tato množina je propojena s Juliovou množinou tak, že každý bod Mandelbrotovy množiny určuje vzhled množiny Juliovy ve vztahu k určitému bodu. Počet iterací určuje barvu čísla.

Dynamické systémy

Atraktor – je definován jako konečný stav systému. Charakterizuje cíl, do kterého směřuje pohyb, např. u kyvadla. Uvedené obrázky této představě příliš neodpovídají, ale specifické fraktály již dynamický pohyb modelují.

Lorenzův atraktor – popisuje chování vodního kola, kdy výsledkem je nekonečná křivka, která nikdy neprotne sebe sama. Připomíná motýlí křídla, která se možná stala symbolem chaosu.

Hénonův atraktor – vzniká neustálým natahováním a ohýbáním fázového prostoru. Přes svou jednoduchost je pro matematiky stále „záhadný“, neboť jednotlivé vzniklé křivky jsou vlastně páry křivek vedle sebe. Bez výpočtu nejde určit, kde se objeví následující bod křivky.

King´s dream – fraktál vytvořený opravdu jen pro radost.

Fraktály v mobilních zařízeních

Existuje mnoho aplikací pro mobilní operační systémy, ve kterých lze fraktály buď editovat, nebo prohlížet v podobě galerií. Díky kvalitě rozlišení a možnosti přiblížení se tak nabízí zajímavá platforma například pro výtvarné hrátky. Přičemž jde stále o matematiku.

Některé vyzkoušené aplikace: Fractile Plus, FractalTree, MandelPad, Fast Fractal (iOS), Fractals (Android), IFS Fractal (Windows Phone), jejich počet stále narůstá. Výhodou je jednoznačně nezávislost na zvoleném systému, pokud se bude hledat nějaký konkrétní fraktál, v rámci BYOD není třeba řešit konkrétní aplikaci, ale cíl.

Autor: Petr Chlebek