Pokračování článku je zaměřeno na grafy a řešení rovnic pomocí tabulkového kalkulátoru.

Excel využijeme i při tvorbě grafů, např. pro výuku statistiky, a v neposlední řadě i při výuce grafického řešení soustav lineárních rovnic. Zde žáci oceňují především to, že pokud mají rýsovat, ne vždy se jim správné řešení kvůli nepřesnosti v rýsování podaří nalézt.

Vycházíme z toho, že žáci se v matematice nejprve učí řešit soustavy rovnic početně různými metodami, a teprve pak přistupujeme ke grafickému řešení. Postup grafického řešení znají také z hodin matematiky, takže ho s nimi při hodinách informatiky stručně pouze zopakujeme. Pak přistoupíme k práci s Excelem.

1) Obě rovnice vyjádří ve tvaru y = ax + b.

2) Připraví si dvě tabulky.

3) Hodnoty x zvolí libovolně (ideálně jedno záporné a jedno kladné číslo). Je dobré, pokud absolutní hodnota zvolených čísel není moc velká.

4) Hodnoty y zapíší ve tvaru vzorce, který si určili (viz bod 1).

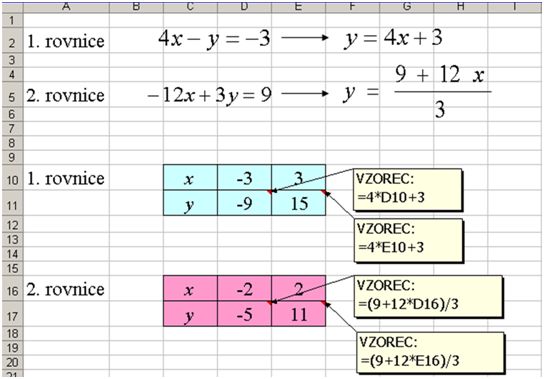
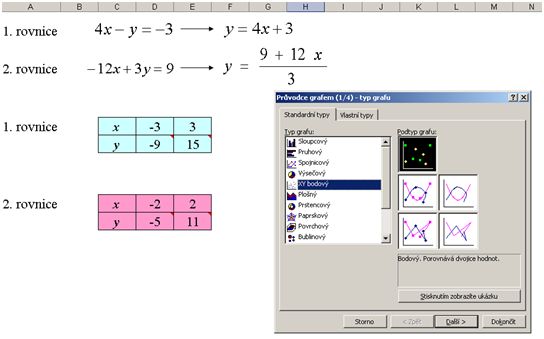
5) Poté můžou přistoupit k tvoření grafu. Ze záložky Standardní typy vyberou XY bodový a kliknou na Další.

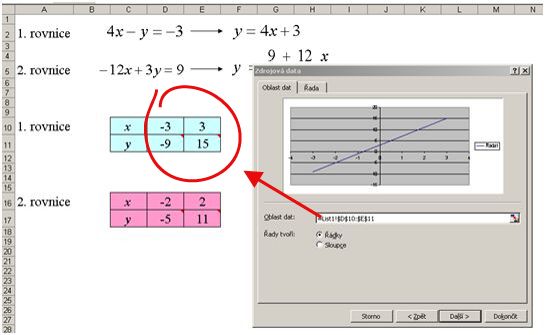
6) Otevře se plovoucí okno s názvem Zdrojová data. Jako oblast dat zvolí hodnoty z tabulky pro první rovnici.

7) Dále přepnou na záložku Řada a pro vytvoření grafu druhé rovnice musí přidat druhou řadu.

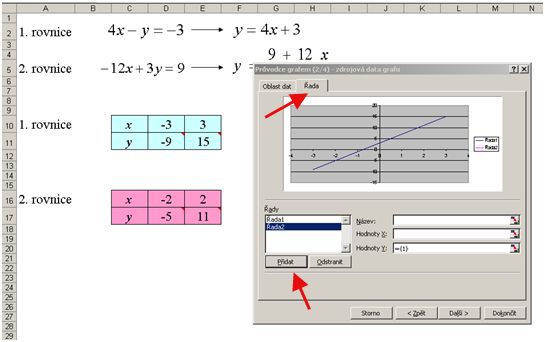
8) Do řádku Hodnoty X musí vybrat oblast pro hodnoty x a do řádku Hodnoty Y oblast pro hodnoty y z druhé tabulky (tabulka pro druhou rovnici). Poté kliknou na Dokončit.

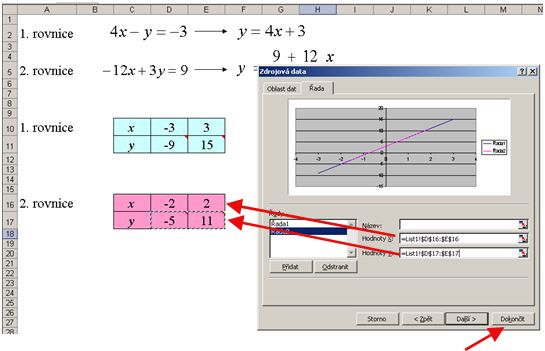
9) Vzhled výsledného grafu mohou upravit podle sebe nebo podle zadání vyučujícího.

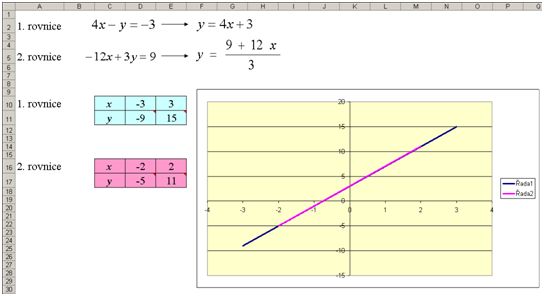
10) O výsledku je dobré vést s žáky diskuzi – co jim vyšlo, co to znamená pro řešení soustavy lineárních rovnic.

Vzhledem k tomu, že při řešení soustav lineárních rovnic mohou vzniknout tři situace, je třeba, aby všechny žáci viděli. Z výše uvedeného vyplynulo, že soustava má nekonečně mnoho řešení, je tedy dobré, aby vytvořili ještě grafy na jedno řešení a žádné řešení.

Jedno řešení

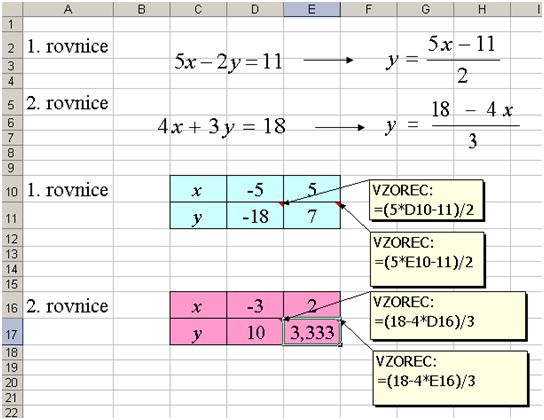
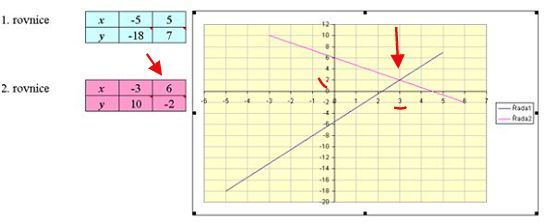
Pokud má soustava jedno řešení, může se stát, že žáci zvolí do tabulky za neznámou x takové hodnoty, že po vytvoření grafu není vidět průsečík (viz obrázek níže). 

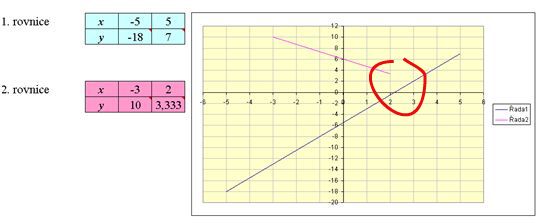
Tato situace opět prověří jejich matematické znalosti (a také představivost), takže je čas na další diskuzi – Co je grafem jednotlivých lineárních rovnic (lineárních funkcí)? [přímka], Jak vypadá přímka? [je nekonečná] = průsečík tedy mají, jen není na grafu vidět. Můžeme se také zkusit zeptat, co je nutné udělat, aby průsečík vidět byl, většinou na to žáci přijdou.

Protože je znázorněná příliš krátká přímka patřící k druhé rovnici, musí upravit hodnoty x v druhé tabulce tak, aby se znázorněná přímka prodloužila. Poté už jen řeknou, jaký je správný výsledek – výsledkem je průsečík přímek.

Žádné řešení

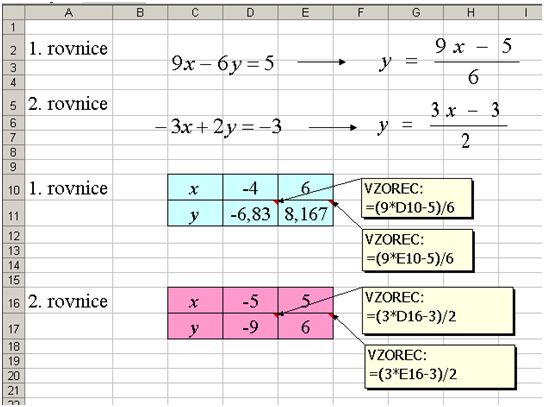
Diskuze – přímky nemají žádný průsečík, takže soustava nemá žádné řešení.

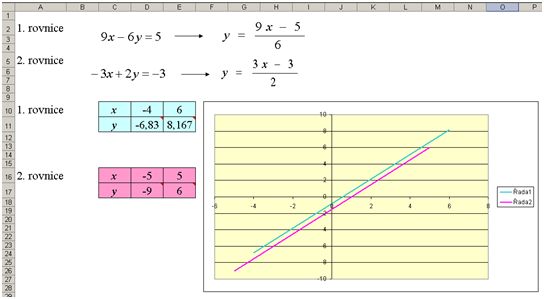
Pokud máme dostatek počítačů, je vhodné, aby každý žák všechna tři řešení vyzkoušel sám. Když sedí u jednoho PC dva žáci, pak je dobré, aby se prostřídali. Ten, který zrovna nepracuje na počítači, může pro kontrolu spočítat soustavy rovnic jinou metodou.

Myslím si, že v moderní době není nutné tvrdošíjně trvat na tom, aby vše bylo narýsováno „ručně“, vždyť zrovna při grafickém řešení soustav rovnic není nejdůležitější, jestli žák umí rýsovat, ale zda ví, jak postupovat, aby na výsledné řešení přišel. Je jedno, jestli za použití pravítka a tužky nebo za použití počítače a programu, který mu s „rýsováním“ pomůže.

Autorka: Radka Rečníková