Několik námětů pro využití programu GEOGEBRA při výuce algebry. Vzhledem k dostupnosti tohoto výborného nástroje, jeho volné šiřitelnosti a možném přístupu přes počítač i tablet je k dispozici aplikace s mnoha možnostmi využití.

Při zavádění pojmu lineární funkce v 9. ročníku narážíme často na problém pochopení „závislosti jedné proměnné na druhé“. Přestože žáci běžně používají vzorce v geometrii, ve fyzice a v chemii, pokud jim chceme závislost zavést jako matematický pojem, připadá jim, že mluvíme o něčem úplně teoretickém.

Začneme tím, že seznámíme žáky s obecným předpisem y=ax+b. Vysvětlíme parametry a a b a naučíme je sestrojit graf lineární funkce. Můžeme vycházet z jejich zkušeností s grafem přímé úměrnosti a navázat na znalosti o něm. Při dalším zkoumání lineární funkce můžeme využít GeoGebru, která žákům umožní vytvářet vlastní grafy funkcí, aniž by tyto rýsovali do sešitů. Práce s GeoGebrou slouží ke zkoumání vlastností funkcí a hledání souvislostí mezi parametry a a b a tvarem grafu funkce.

Pokud žáky naučíme základní ovládání GeoGebry, je možné je nechat s funkcemi experimentovat. V podstatě stačí seznámit je s možností zadávat funkce pomocí vstupního pole. Důležitou pomůckou je i zapnuté algebraické okno, ve kterém se objevují předpisy jednotlivých objektů v nákresně.

Dalším pomocníkem je pro ně určitě změna barvy grafu funkce ve vlastnostech objektů. Případně popis objektu. Zápis funkce v algebraickém okně má stejnou barvu jako graf funkce, což je výborná pomůcka pro orientaci v objektech.

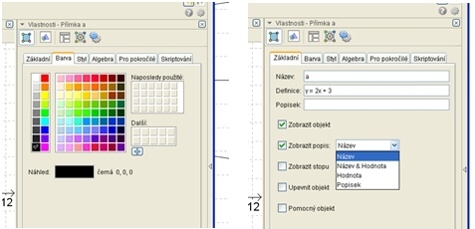
První úkol zní:

Narýsuj grafy funkcí y=2x; y=x; y=3x; y=0,5x; y=0,2x. Důležitá je funkce y=x, tu přebarvi na červenou. Funkce, které mají graf „nad ní“, zobraz modře, funkce, které mají graf „pod ní“, zobraz zeleně.

Výsledná práce může vypadat třeba takto:

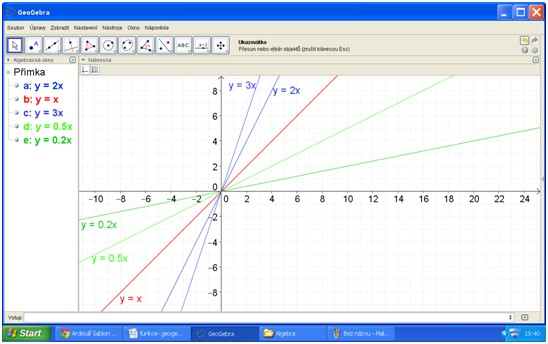
Pokud tuto práci zvládnou, můžeme pokládat doplňující otázky.

• Co je společné pro modré/zelené funkce?
• Zkus vymyslet předpis další funkce, která by mohla být modrá/zelená?
• Na čem závisí strmost funkce?

Důležité je ale, že žáci sami objeví závislost naklonění grafu na parametru a.

Další úkol je:

Narýsuj grafy funkcí y=2x; y=-2x; y=-0,5x; y=0,5x; y=-x;y=x. Funkce se záporným lineárním členem přebarvi zeleně, funkce s kladným lineárním členem zobraz modře.

Práce žáků může vypadat třeba takto:

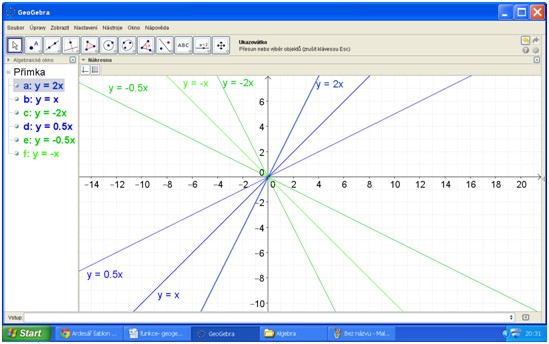
Následují otázky typu:

• Co spojuje modré/zelené funkce?
• Zkus vymyslet předpis pro další modré/zelené funkce.

Závěrem můžeme se žáky pojmenovat funkce jako rostoucí a klesající a vysvětlit si závislost této vlastnosti u lineární funkce na parametru a.

V tuto chvíli je čas začít se zabývat parametrem b.

Začneme jednoduchým úkolem:

Sestroj grafy funkcí y=2x; y=2x+1; y=2x-1; y=2x+2; y=2x-2,5. Všimni si, jakým bodem na ose y jednotlivé grafy prochází. Body na nákresně vyznač.

Práce žáků vypadá takto:

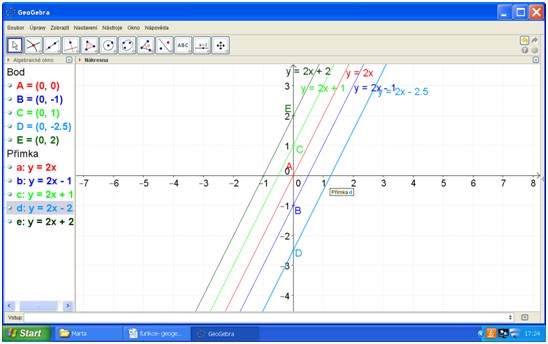
Při rozboru vypracovaného úkolu se ještě můžeme vrátit k lineárnímu členu a. Případné naše otázky mohou znít:

• Co je zajímavé na grafech všech funkcí?
• Čím je způsobena jejich rovnoběžnost?
• Umíš navrhnout další funkci, která bude mít s danými funkcemi rovnoběžný graf?

Tím upozorníme žáky opět na vztah mezi a a „strmostí“ funkce.

Otázky týkající se absolutního členu mohou být:

• Co mají společné průsečíky grafů jednotlivých funkcí s předpisy těchto funkcí?
• Proč všechny průsečíky mají x-ovou souřadnici nulovou?
• Vyvoď z obecné rovnice y=ax+b předpis pro průsečík s osou y.

Závěrem je určení průsečíku lineární funkce s osou y pro libovolný předpis, aniž by bylo třeba graf konstruovat.

Trochu těžší je pro žáky určit průsečík s osou x, ale i to je možné zvládnout. Obdobně zadáme „šikovné“ funkce, a žáci hledají průsečík s osou x.

Sestroj grafy funkcí y=0,5x-1; y=-2x-5; y=-x+4; y=3x-1,5. Označ průsečíky grafů s osou x.

Výsledná práce:

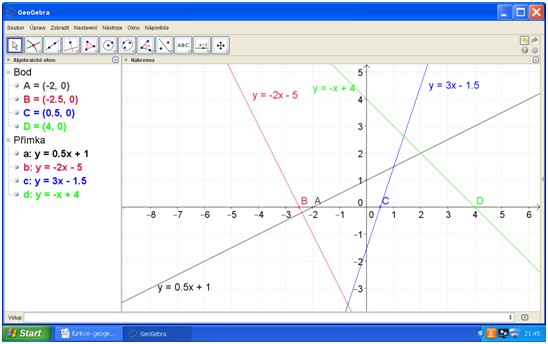
A ptáme se dál:

• Co mají společného všechny průsečíky?
• Proč všechny průsečíky mají y-ovou souřadnici nulovou?
• Vyvoď z obecné rovnice y=ax+b předpis pro průsečík s osou x.

V tuto chvíli už jsou žáci schopni vyšetřit průběh lineární funkce – monotónnost a průsečíky s osami. Měli by být schopni navrhnout předpis funkce, která je rovnoběžná nebo která má stejný průsečík s osou y.

Dalším zajímavým úkolem pro žáky může být i řešení soustavy dvou lineárních rovnic. GeoGebra umí samozřejmě vyčíslit jakoukoli rovnici o dvou neznámých.

Vyřeš soustavu rovnic x-2y=0; (x+3)/2=(1-y)/4. Obě rovnice zadej do vstupního pole a najdi v nákresně řešení.

Jednoduché řešení může vypadat třeba takto:

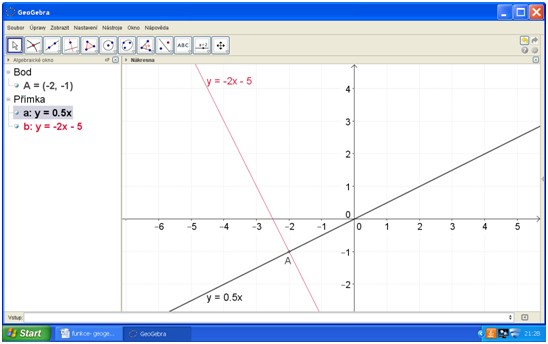
Následují otázky:

• V co se změnily obě rovnice? Co je tedy vlastně rovnice o dvou neznámých?
• Co je řešením soustavy dvou rovnic?
• Jak bychom poznali soustavu, která nemá žádné řešení?
• Jak bychom poznali soustavu, která má nekonečně mnoho řešení?

Toto je jen pár námětů na využití programu GeoGebra při výuce algebry na základní škole. Její výhodou je dostupnost a velmi jednoduché ovládání. V podstatě na její využití stačí pouze připojení k internetu a maximálně desetiminutová ukázka základního ovládání. Věřím, že žáky tato forma zaujme a že pochopí pojem funkce jako nedílné součásti matematiky.

Autorka: Marta Pincová